normalizeLPF - Normalize by Low-pass filter
Normalizes image time series using low-pass filter
Description
This function can be used to normalise channels (ΔF/F or ΔR/R), or to do a low-pass filtering.
Input
This function accepts only image time series as input with dimensions Y, X and T.
The algorithm
This function applies low pass filters at two cut-off frequencies (set in the function's parameters). Then, these two low-passed signals are either subtracted or divided which results in the normalized signal (R) expressed as ΔR or ΔR/R, respectively.
The function applies a 4th-order low-pass Butterworth filter with 3dB cut-off frequencies freqHigh and freqLow. This yields two low-passed signals S_lwpfreqHigh and S_lwpfreqLow. Then, if the parameter Normalize is set to True, the signals are divided as:
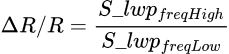
otherwise, the signals are subtracted:
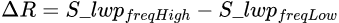
Output
The output of this function is a numerical matrix with dimensions Y,X and T containing the data filtered and normalized.
Parameters
The parameter of this function are the following:
Sets the value (in Hertz) of the low frequency cut-off.
The LowCutOffHz value ranges from zero to the Nyquist (half the sample rate).
Note
If this value is set to zero, the output will be a low-passed signal at cut-off frequency HighCutOffHz.
Sets the value (in Hertz) of the high frequency cut-off.
The HighCutOffHz value must be a positive number between the LowCutOffHz value and the Nyquist (half the sample rate).
Sets this parameter to True (default) to return the output signal (R) as ΔR/R, otherwise set to False to return the output signal as ΔR (see the algorithm) sections for details).
Set this parameter to True to apply a double exponential fit to the input signal prior to the filtering. In the majority of cases, this is not necessary. However, in cases where the temperature of the illumination source of the imaging system is poorly managed, a signal decay may occur. Thus, the exponential fit can be applied to fix this issue.